Structure and principle design of sugar candied low-pass filter
The candied fruit low-pass filter is widely used in coaxial systems due to its simple structure, low insertion loss, and high power handling capability. It is one of the most common types of coaxial low-pass filters. The design of this filter follows the principles of high-low impedance line low-pass filters. However, because the candied fruit low-pass filter is a three-dimensional structure, the edge capacitance between the low-impedance lines cannot be ignored. This makes the standard high-low impedance interconnection model less accurate for determining the physical dimensions of the filter. In this article, we present a more precise and practical design method for the candied fruit low-pass filter.
1. Design Challenges and Countermeasures for Candied Fruit Low-Pass Filters
1.1 Discontinuity Analysis of Candied Fruit Low-Pass Filters
The typical structure of a candied fruit low-pass filter is shown in Figure 1. At lower frequencies, the length of the sugar cane-like structures is relatively long, making the edge capacitance small compared to the overall low-impedance line. In such cases, a simple high-low impedance cascade model can be used to approximate the behavior of the filter. However, as the operating frequency increases, the size of the structure decreases, causing the edge capacitance to become more significant and no longer negligible. This leads to inaccuracies when using the traditional high-low impedance model. Therefore, it is essential to account for the edge capacitance during the design process.


Figure 1: Typical low-pass structure and principle of candied fruit
When initially analyzing the design of a candied fruit low-pass filter, two main factors were considered:
- Edge capacitance
- Capacitive coupling between the low-impedance lines
After building a model based on these assumptions, the simulation results showed a high-frequency response, but the standing wave ratio was not ideal. Upon examining the field distribution, it was observed that only the edge capacitance field was prominent between the sugar-cane-like structures. There was little to no plate capacitance or coupling field between the low-impedance lines. This may be due to the fact that the low-impedance lines are connected to high-impedance lines, resulting in an equivalent potential and thus no capacitor formation. Based on this, the focus should be on modeling the edge capacitance rather than other effects. Hence, accurately modeling the edge capacitance is crucial for achieving a better design.
1.2 Acquisition of Edge Capacitance
Edge capacitance arises at the step discontinuities between high- and low-impedance lines. The dimensions of these lines are typically fixed during the design phase. Using this information, a ladder structure can be created in HFSS to simulate the step discontinuities and generate an S2P file. This file captures the electromagnetic behavior of the discontinuities accurately. The S2P file is then imported into ADS to build a circuit model that represents the low-pass characteristics of the candied fruit filter.
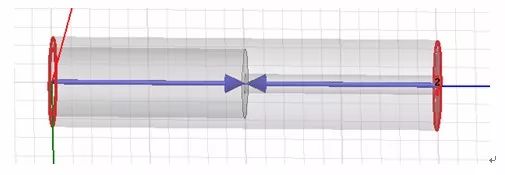
Figure 2: Steps for discontinuity modeling
2. Design Example of a Candied Fruit Low-Pass Filter
Based on the above approach, the design process of a candied fruit low-pass filter can be divided into three main steps:
- Simulate the high- and low-impedance lines to obtain the parameters of the step discontinuities.
- Create a model in ADS to extract key size data from 3D simulations.
- Build a 3D simulation model in HFSS to verify the results.
2.1 Size Planning and Simulation of Step Discontinuities
To illustrate the design process, we use a 15 GHz example. A model parameter setup is provided in Table 1.
Table 1: Key Size Planning for Candied Fruit Filters

Using the data from Table 1, a step discontinuity model is created, and an S2P file is generated through simulation.
2.2 Building a Model in ADS to Obtain Key Size Data
As described earlier, a model is built in ADS, as shown in Figure 4. The step discontinuity is represented by the S2P file. Parameters are adjusted in ADS to achieve the desired performance. The detailed simulation results are presented in Figure 3.
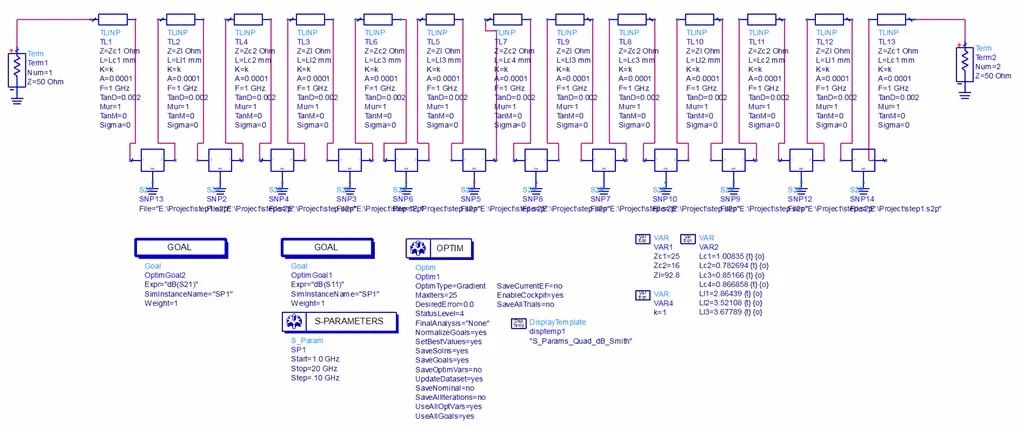
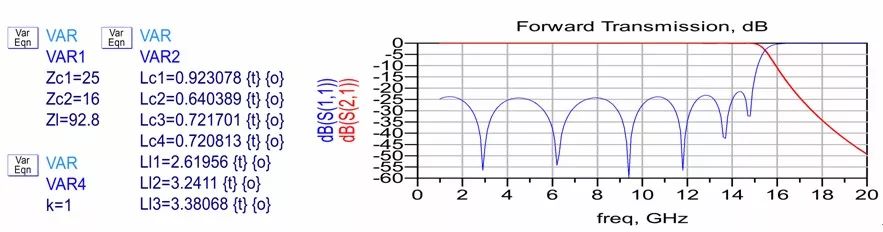
Figure 3: ADS model and simulation results of the candied fruit filter
2.3 Building a 3D Model in HFSS to Verify the Design
Based on the results from the previous step, a 3D model is constructed in HFSS, as shown in Figure 4. The simulation results are very promising, with minimal need for optimization, confirming the accuracy of the ADS model.
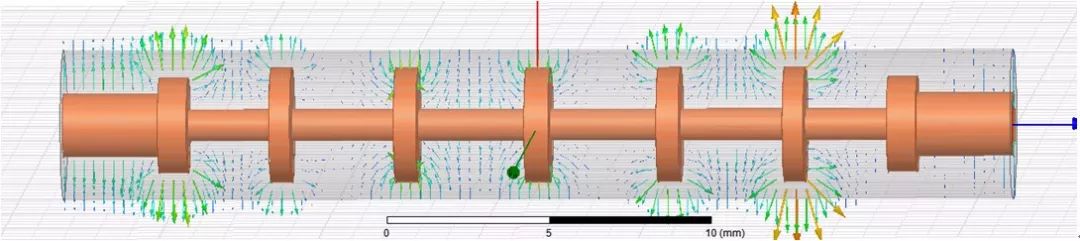

Figure 4: 3D simulation model and one simulation result
Wall-Mounted Advertising Display
wall mounted digital advertising screen, horizontal Advertising display, wall mounted digital advertising display
Guangdong Elieken Electronic Technology Co.,Ltd. , https://www.elieken.com